⼏个有趣的位操作
1
2
| ('a' | ' ') = 'a'
('A' | ' ') = 'a'
|
原理:
1
2
3
4
5
6
7
| ------小写-------
a 1100001
b 1100010
c 1100011
d 1100100
y 1111001
z 1111010
|
1
2
3
4
5
6
7
| ------大写-------
A 1000001
B 1000010
C 1000011
D 1000100
Y 1011001
Z 1011010
|
1
2
| ------ ' ' ------
0100000
|
- 利⽤与操作 & 和下划线将英⽂字符转换为⼤写
(‘b’ & ‘’) = ‘B’
(‘B’ & ‘’) = ‘B’
1
2
| ------ '_' ------
1011111
|
1
2
| ('d' ^ ' ') = 'D'
('D' ^ ' ') = 'd'
|
1
2
3
4
| int x = -1, y = 2;
bool f = ((x ^ y) < 0); // true
int x = 3, y = 2;
bool f = ((x ^ y) < 0); // false
|
这个技巧还是很实⽤的,利⽤的是补码编码的符号位
1
2
3
4
5
| int a = 1, b = 2;
a ^= b;
b ^= a;
a ^= b;
// 现在 a = 2, b = 1
|
1
2
3
| int n = 1;
n = -~n;
// 现在 n = 2
|
1
2
3
| int n = 2;
n = ~-n;
// 现在 n = 1
|
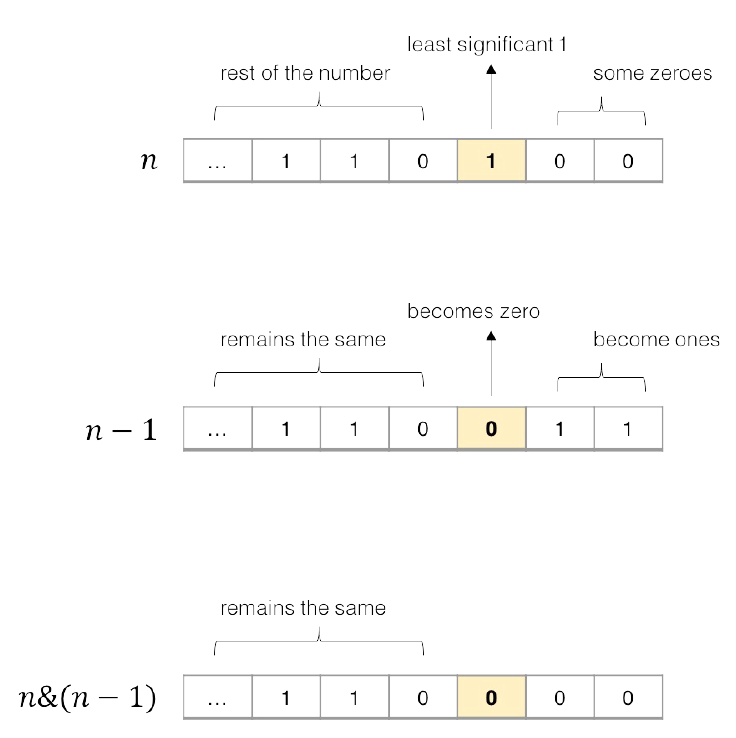
算法常⽤操作 n&(n-1)
这个操作是算法中常⻅的,作⽤是消除数字 n 的⼆进制表⽰中的最后⼀个 1。
算法题
计算汉明权重(Hamming Weight)

方法一:因为 n & (n - 1) 可以消除最后⼀个 1,所以可以⽤⼀个循环不停地消除 1 同时计数,直到 n 变成 0 为⽌。
1
2
3
4
5
6
7
8
| int hammingWeight(uint32_t n) {
int res = 0;
while (n != 0) {
n = n & (n - 1);
res++;
}
return res;
}
|
判断⼀个数是不是 2 的指数
⼀个数如果是 2 的指数,那么它的⼆进制表⽰⼀定只含有⼀个 1。
如果使⽤位运算技巧就很简单了(注意运算符优先级,括号不可以省略):
1
2
3
4
| bool isPowerOfTwo(int n) {
if (n <= 0) return false;
return (n & (n - 1)) == 0;
}
|
字符串转整数
1
2
3
4
5
6
7
| string s = "458";
int n = 0;
for (int i = 0; i < s.size(); i++) {
char c = s[i];
n = 10 * n + (c - '0');
}
// n 现在就等于 458
|
坑: (c -‘0’) 的这个括号不能省略,否则可能造成整型溢出。
因为变量 c 是⼀个 ASCII 码,如果不加括号就会先加后减,想象⼀下 s 如果接近 INT_MAX,就会溢出。所以⽤括号保证先减后加才⾏。

