队列 API 如下:
1
2
3
4
5
6
7
8
9
10
class MyQueue {
/** 添加元素到队尾 */
public void push(int x);
/** 删除队头的元素并返回 */
public int pop();
/** 返回队头元素 */
public int peek();
/** 判断队列是否为空 */
public boolean empty();
}
⽤栈实现队列
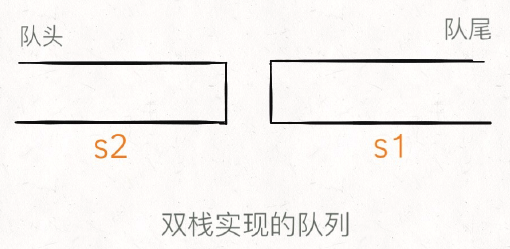
使⽤两个栈 s1, s2 就能实现⼀个队列的功能(这样放置栈可能更容易理解):
1
2
3
4
5
6
7
8
class MyQueue {
private Stack<Integer> s1, s2;
public MyQueue() {
s1 = new Stack<>();
s2 = new Stack<>();
}
// ...
}
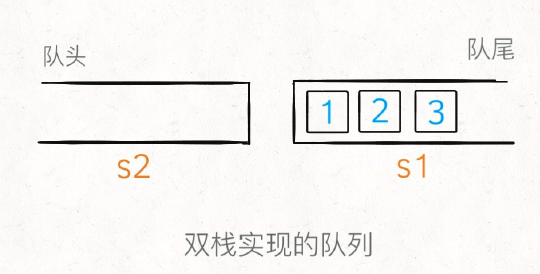
当调⽤ push 让元素⼊队时,只要把元素压⼊ s1 即可,⽐如说 push 进 3 个元素分别是 1,2,3,那么底层结构就是这样:
1
2
3
4
/** 添加元素到队尾 */
public void push(int x) {
s1.push(x);
}
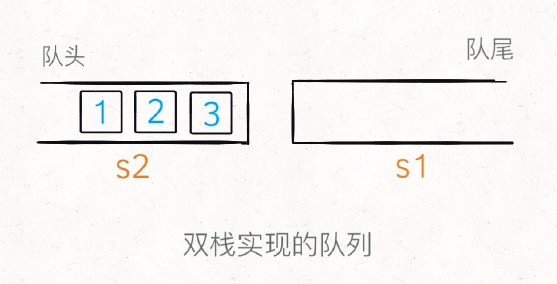
那么如果这时候使⽤ peek 查看队头的元素怎么办呢?按道理队头元素应该是 1,但是在 s1 中 1 被压在栈底,现在就要轮到 s2 起到⼀个中转的作⽤了:当 s2 为空时,可以把 s1 的所有元素取出再添加进 s2 ,这时候 s2 中元素就是先进先出顺序了。
1
2
3
4
5
6
7
8
/** 返回队头元素 */
public int peek() {
if (s2.isEmpty())
// 把 s1 元素压⼊ s2
while (!s1.isEmpty())
s2.push(s1.pop());
return s2.peek();
}
同理,对于 pop 操作,只要操作 s2 就可以了。
1
2
3
4
5
6
/** 删除队头的元素并返回 */
public int pop() {
// 先调⽤ peek 保证 s2 ⾮空
peek();
return s2.pop();
}
最后,如何判断队列是否为空呢?如果两个栈都为空的话,就说明队列为空:
1
2
3
4
/** 判断队列是否为空 */
public boolean empty() {
return s1.isEmpty() && s2.isEmpty();
}
⾄此,就⽤栈结构实现了⼀个队列,核⼼思想是利⽤两个栈互相配合。
值得⼀提的是,这⼏个操作的时间复杂度是多少呢?有点意思的是 peek 操作,调⽤它时可能触发 while 循环,这样的话时间复杂度是 O(N),但是⼤部分情况下 while 循环不会被触发,时间复杂度是 O(1)。由于 pop 操作调⽤了 peek ,它的时间复杂度和 peek 相同。像这种情况,可以说它们的最坏时间复杂度是 O(N),因为包含 while 循环,可能需要从 s1 往 s2 搬移元素。