快慢指针
快慢指针⼀般都初始化指向链表的头结点 head,前进时快指针 fast 在前,慢指针 slow 在后,巧妙解决⼀些链表中的问题。
判定链表中是否含有环
单链表的特点是每个节点只知道下⼀个节点,所以⼀个指针的话⽆法判断链表中是否含有环的。
经典解法就是⽤两个指针,⼀个跑得快,⼀个跑得慢。如果不含有环,跑得快的那个指针最终会遇到 null,说明链表不含环;如果含有环,快指针最终会超慢指针⼀圈,和慢指针相遇,说明链表含有环。
1
2
3
4
5
6
7
8
9
10
boolean hasCycle(ListNode head) {
ListNode fast, slow;
fast = slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) return true;
}
return false;
}
已知链表中含有环,返回这个环的起始位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ListNode detectCycle(ListNode head) {
ListNode fast, slow;
fast = slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) break;
}
// 上⾯的代码类似 hasCycle 函数
slow = head;
while (slow != fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
可以看到,当快慢指针相遇时,让其中任⼀个指针指向头节点,然后让它俩以相同速度前进,再次相遇时所在的节点位置就是环开始的位置。
第⼀次相遇时,假设慢指针 slow ⾛了 k 步,那么快指针 fast ⼀定⾛了 2k 步,也就是说⽐ slow 多⾛了 k 步(也就是环的⻓度)。
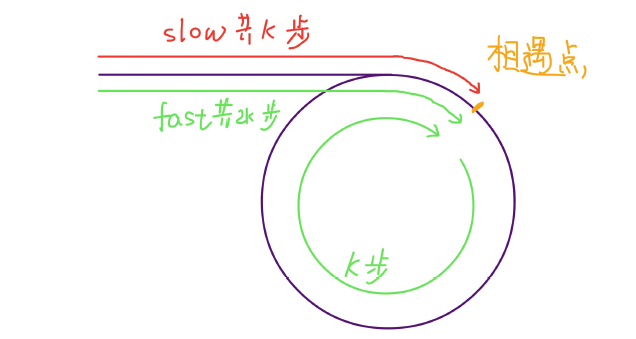
设相遇点距环的起点的距离为 m,那么环的起点距头结点 head 的距离为 k - m,也就是说如果从 head 前进 k - m 步就能到达环起点。
巧的是,如果从相遇点继续前进 k - m 步,也恰好到达环起点。
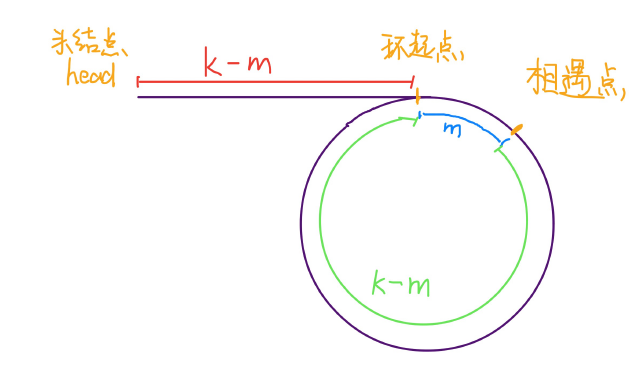
所以,只要我们把快慢指针中的任⼀个重新指向 head,然后两个指针同速前进,k - m 步后就会相遇,相遇之处就是环的起点了。
寻找链表的中点
可以让快指针⼀次前进两步,慢指针⼀次前进⼀步,当快指针到达链表尽头时,慢指针就处于链表的中间位置。
1
2
3
4
5
6
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
// slow 就在中间位置
return slow;
当链表的⻓度是奇数时,slow 恰巧停在中点位置;如果⻓度是偶数,slow 最终的位置是中间偏右。
寻找链表中点的⼀个重要作⽤是对链表进⾏归并排序。
回想数组的归并排序:求中点索引递归地把数组⼆分,最后合并两个有序数组。对于链表,合并两个有序链表是很简单的,难点就在于⼆分。
寻找链表的倒数第 k 个元素
使⽤快慢指针,让快指针先⾛ k 步,然后快慢指针开始同速前进。 这样当快指针⾛到链表末尾 null 时,慢指针所在的位置就是倒数第 k 个链表节点(为了简化,假设 k 不会超过链表⻓度):
1
2
3
4
5
6
7
8
9
ListNode slow, fast;
slow = fast = head;
while (k-- > 0)
fast = fast.next;
while (fast != null) {
slow = slow.next;
fast = fast.next;
}
return slow;
左右指针
左右指针在数组中实际是指两个索引值,⼀般初始化为 left = 0, right = nums.length - 1 。
⼆分查找
两数之和
给定一个已按照升序排列的有序数组,找到两个数使得它们相加之和等于目标值。
只要数组有序,就应该想到双指针技巧。这道题的解法有点类似⼆分查找, 通过调节 left 和 right 可以调整 sum 的⼤⼩:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int[] twoSum(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left < right) {
int sum = nums[left] + nums[right];
if (sum == target) {
// 题⽬要求的索引是从 1 开始的
return new int[]{left + 1, right + 1};
} else if (sum < target) {
left++; // 让 sum ⼤⼀点
} else if (sum > target) {
right--; // 让 sum ⼩⼀点
}
}
return new int[]{-1, -1};
}
反转数组
1
2
3
4
5
6
7
8
9
10
11
void reverse(int[] nums) {
int left = 0;
int right = nums.length - 1;
while (left < right) {
// swap(nums[left], nums[right])
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
left++; right--;
}
}