栈（stack）是很简单的⼀种数据结构，先进后出的逻辑顺序，符合某些问题的特点，⽐如说函数调⽤栈。
单调栈实际上就是栈，只是利⽤了⼀些巧妙的逻辑，使得每次新元素⼊栈后，栈内的元素都保持有序（单调递增或单调递减）。
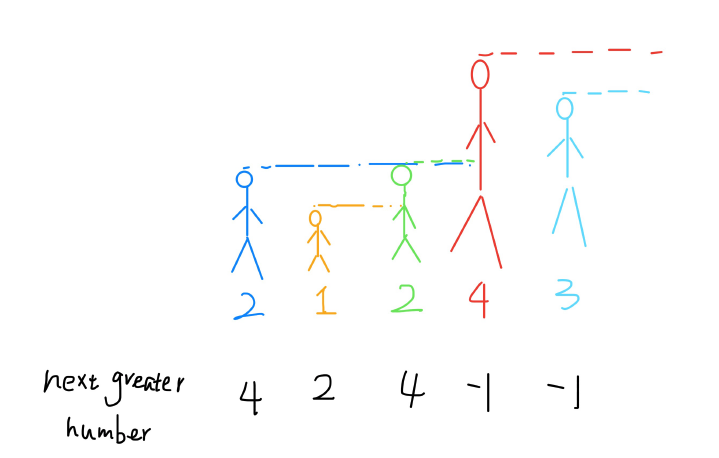
单调栈⽤途不太⼴泛，只处理⼀种典型的问题，叫做 Next Greater Element。Next Greater Number 的原始问题：给定⼀个数组，返回⼀个等⻓的数组，对应索引存储着下⼀个更⼤元素，如果没有更⼤的元素，就存
-1。例如：
1
原数组 [2,1,2,4,3]，返回数组 [4,2,4,-1,-1]
1
2
3
4
5
6
7
8
9
10
11
12
public static int[] nextGreaterElement(int[] nums) {
int[] ans = new int[nums.length]; // 存放答案的数组
Stack<Integer> s = new Stack<>();
for (int i = nums.length - 1; i >= 0; i--) { // 倒着往栈⾥放
while (!s.empty() && s.peek() <= nums[i]) { // 判定个⼦⾼矮
s.pop(); // 矮个起开，反正也被挡着了。。。
}
ans[i] = s.empty() ? -1 : s.peek(); // 这个元素⾝后的第⼀个⾼个
s.push(nums[i]); // 进队，接受之后的⾝⾼判定吧！
}
return ans;
}
这个算法的时间复杂度不是那么直观，如果看到 for 循环嵌套 while 循环，可能认为这个算法的复杂度也是 O(n^2)，但是实际上这个算法的复杂度只有 O(n)。
分析它的时间复杂度，要从整体来看：总共有 n 个元素，每个元素都被 push ⼊栈了⼀次，⽽最多会被 pop ⼀次，没有任何冗余操作。所以总的计算规模是和元素规模 n 成正⽐的，也就是 O(n) 的复杂度。
如何处理「循环数组」
同样是 Next Greater Number，现在假设数组是个环形的，如何处理？ 输入数组 [2,1,2,4,3]，返回数组 [4,2,4,-1,4]。拥有了环形属性，最后 ⼀个元素 3 绕了⼀圈后找到了⽐⾃⼰⼤的元素 4。
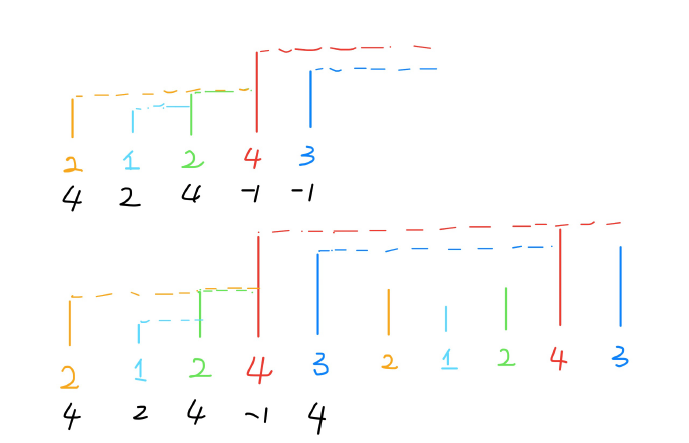
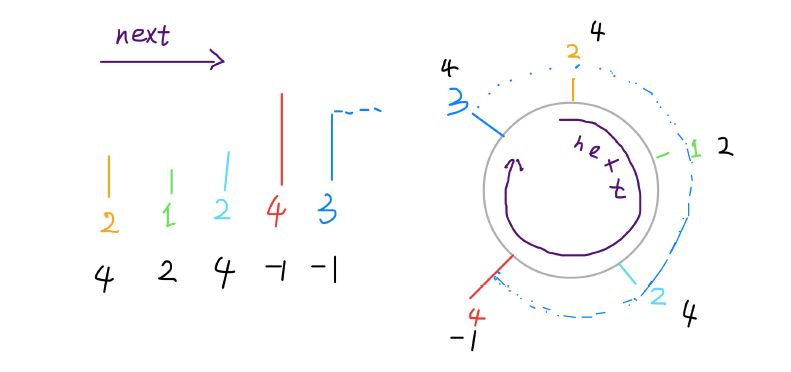思路：将原始数组“翻倍”，就是在后⾯再接⼀个原始数组，这样的话，按照之前“⽐⾝⾼”的流程，每个元素不仅可以⽐较⾃⼰右边的元素，⽽且也可以和左边的元素⽐较了。
1
2
3
4
5
6
7
8
9
10
11
12
13
vector<int> nextGreaterElements(vector<int>& nums) {
int n = nums.size();
vector<int> res(n); // 存放结果
stack<int> s;
// 假装这个数组⻓度翻倍了
for (int i = 2 * n - 1; i >= 0; i--) {
while (!s.empty() && s.top() <= nums[i % n])
s.pop();
res[i % n] = s.empty() ? -1 : s.top();
s.push(nums[i % n]);
}
return res;
}
