「回溯算法」实际上是一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就 “回溯” 返回，尝试别的路径。回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为 “回溯点”。许多复杂的，规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。
回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。
算法框架
解决一个回溯问题，实际上就是一个决策树的遍历过程。只需要思考 3 个问题：
- 路径：即已经做出的选择。
- 选择列表：即当前可以做的选择。
- 结束条件：即到达决策树底层，无法再做选择的条件。
代码方面，回溯算法的框架：
1
2
3
4
5
6
7
8
9
10
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」，特别简单。
示例
全排列问题
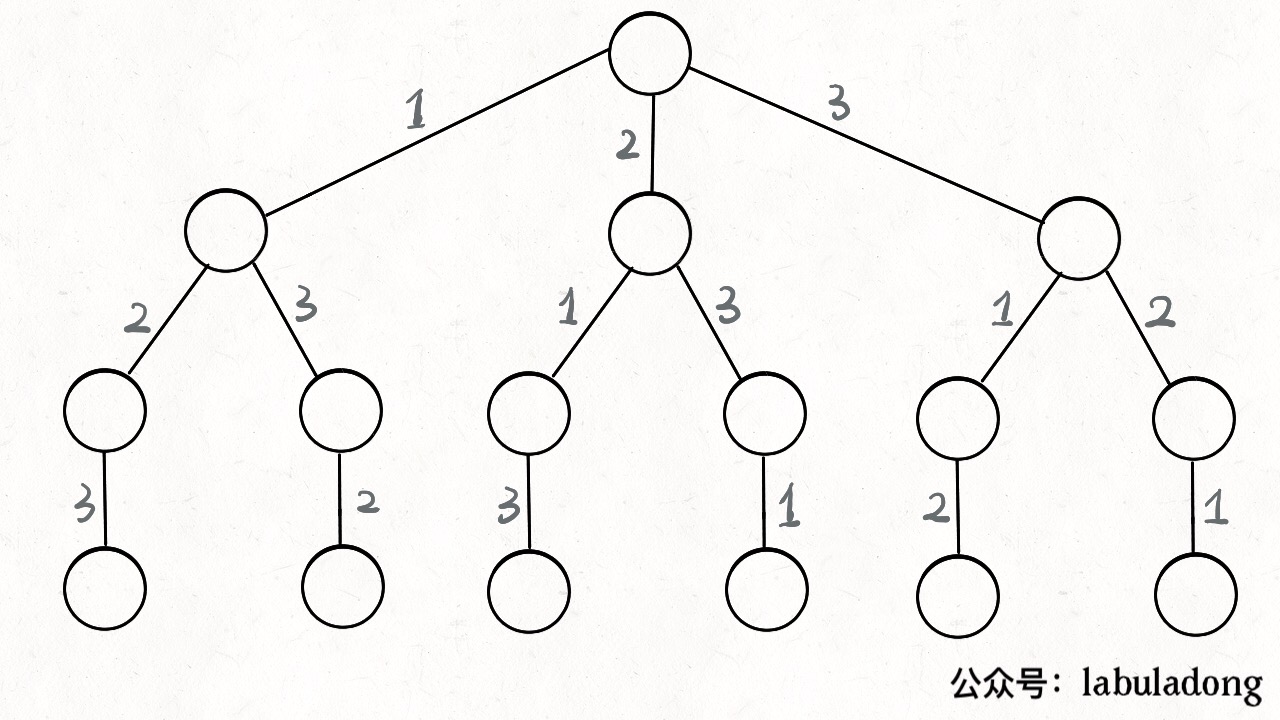只要从根遍历这棵树，记录路径上的数字，其实就是所有的全排列。不妨把这棵树称为回溯算法的「决策树」。
