分布式存储系统通常会通过维护多个副本来进行容错，以提高系统的可用性。这就引出了分布式存储系统的核心问题一如何保证多个副本的一致性？
对于一致性，可以分别从客户端和服务端两个不同的视角来理解。从客户端来看，一致性主要是指多并发访问时如何获取更新过的数据的问题。从服务端来看，则是更新如何复制分布到整个系统，以保证数据最终的一致性。因此，可以从两个角度来查看一致性模型：以数据为中心的一致性模型和以用户为中心的一致性模型。
以数据为中心的一致性模型
实现以下这几种一致性模型的难度会依次递减，对一致性强度的要求也依次递减。
严格一致性（Strong Consistency)
任何一次读都能读到某个数据的最近一次写的数据。系统中的所有进程，看到的操作顺序，都和全局时钟下的顺序一致。简言之，在任意时刻，所有节点中的数据是一样的。
严格一致性也称强一致性，原子一致性或者是可线性化（Linearizability)，是要求最高的一致性模型。严格一致性的要求具体如下。
- 任何一次读都能读到某个数据的最近一次写的数据。
- 系统中的所有进程，看到的操作顺序，都与全局时钟下的顺序一致。
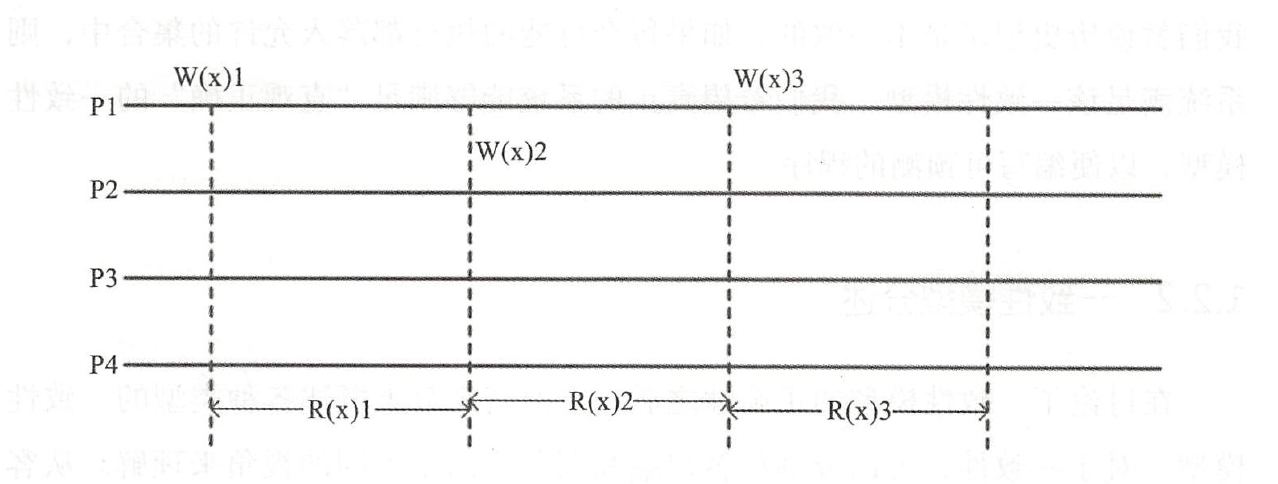在时间轴上，一旦数据 x 被重新写入了，其他进程读到的要求就必须是最新的值。
对于严格一致性的存储器，要求写操作在任一时刻对所有的进程都是可见的，同时还要维护一个绝对全局时间顺序。一旦存储器中的值发生改变，那么不管读写之间的事件间隔有多小，不管是哪个进程执行了读操作，也不管进程在何处，以后读出的都是新更改的值。同样，如果执行了读操作，那么不管后面的写操作有多迅速，该读操作仍应读出原来的值。
传统意义上，单处理机遵守严格一致性。但是在分布式计算机系统中为每个操作都分配一个准确的全局时间戳是不可能实现的。因此，严格一致性，只是存在于理论中的一致性模型。
幸运的是，通常的编程方式是语句执行的确切时间（实际上是存储器访问的时间）并不重要，而当事件（读或写）的顺序至关重要时，可以使用信号量等方法实现同步操作。接受这种意见意味着采用较弱的一致性模式来编程。
按照定义来看，强一致模型是可组合的，也就是说如果一个操作由两个满足强一致的子操作组成，那么父操作也是强一致的。强一致提供了－系列很好的特性，也非常易于理解，但问题在于它基本很难得到高效的实现。因此，研究人员放松了要求，从而得到了在单机多线程环境下实际上普遍存在的顺序一致性模型。
线性一致性
线性一致性，也称原子一致性或外部一致性，介于严格一致性和连续一致性之间。
对于线性一致性，假设每个操作都从松同步的全局时钟那里接收到了一个时间戳。当且仅当这些操作完成得就如同它们是连续执行的且每个操作都像是按照既定的顺序完成的一样时，我们才称操作是线性的。此外，如果一个操作的时间戳在另一个操作之前，那么该操作的执行顺序也该在另一个之前。举个例子，假设一个客户端在 t1 时刻完成了一次写操作，那么在 t2 （假设t2>t1 ）时刻读到的数据至少要和上一次写操作完成时一样新。然而，该读操作可能要在 t3 时刻才完成，此时返回在 t2 时刻开始读的数据相对（t3）就有些陈旧了。
顺序序一致性（Sequential Consistency)
顺序一致性，也称为可序列化，比严格一致性要求弱一点，但也是能够实现的最高级别的一致性模型。
因为全局时钟导致严格一致性很难实现，因此顺序一致性放弃了全局时钟的约束，改为分布式逻辑时钟实现。顺序一致性是指所有的进程都以相同的顺序看到所有的修改。读操作未必能够及时得到此前其他进程对同一数据的写更新，但是每个进程读到的该数据不同值的顺序却是一致的。
可见，顺序一致性在顺序要求上并没有那么严格，它只要求系统中的所有进程达成自己认为的一致就可以了，即“错的话一起错，对的话一起对”，且不违反程序的顺序即可，并不需要整个全局顺序保持一致。
图 a 满足顺序一致性，但是不满足强一致性。原因在于，从全局时钟的观点来看，P2 进程对变量 X 的读操作在 P1 进程对变量 X 的写操作之后，然而读出来的却是旧的数据。但是这个图却是满足顺序一致性的，因为两个进程P1、P2的一致性并没有冲突。从这两个进程的角度来看，顺序应该是这样的： Write(y,2）→ Read(x,O）→ Write(x,4）→ Read(y,2），每个进程内部的读写顺序都是合理的，但是显然这个顺序与全局时钟下看到的顺序并不一样。
图 b 满足强一致性，因为每个读操作都读到了该变量最新写的结果，同时两个进程看到的操作顺序与全局时钟的顺序一样，都是 Write(y,2 ）→ Read(x,4）→ Write(x,4）→ Read(y,2 ）
图 3c 不满足顺序一致性当然也就不满足强一致性了。因为从进程 P1 的角度来看，它对变量 Y 的读操作返回了结果0 。也就是说， P1 进程的对变量 Y 的读操作在 P2 进程对变量Y 的写操作之前，这意味着它认为的顺序是这样的： Write(x,4）→ Read(y,O）→ Write(y,2 ）→ Read(x,O），显然这个顺序是不能满足的，因为最后一个对变量 x 的读操作读出来的也是旧的数据。因此这个顺序是有冲突的，不满足顺序一致性。
通常，满足顺序一致性的存储系统需要一个额外的逻辑时钟服务。
因果一致性（ Causal Consistency)
这里提到的因果关系专指 Lamport 在 “Time,Clocks,and the Ordering of Events in a Distributed System” 论文中描述的 happen-before 关系及其传递闭包，简单地说，因果关系可以描述成如下情况。
- 本地顺序：本进程中，事件执行的顺序即为本地因果顺序。
- 异地顺序：如果读操作返回的是写操作的值，那么该写操作在顺序上一定在读操作之前。
- 闭包传递：与时钟向量里面定义的一样，如果
a → b且b → c，那么肯定也有a → c。
否则，操作之间的关系为并发（ Concurrent ）关系。对于具有潜在因果关系的写操作，所有进程看到的执行顺序应相同。并发写操作（没有因果关系）在不同主机上被看到的顺序可以不同。不严格地说，因果一致性弱于顺序一致性。
在 InfoQ 分享的腾讯朋友圈的设计中，腾讯在设计数据一致性的时候，使用了因果一致性这个模型，用于保证对同一条朋友圈的回复的一致性，比如下面这样的情况。 A 发了朋友圈，内容为梅里雪山的图片。 B 针对 A 的内容回复了评论：“这是哪里？” C 针对 B 的评论进行了回复：“这是梅里雪山” 。 那么，这条朋友圈的显示中，显然 C 针对 B 的评论，应该在 B 的评论之后，这是一个因果关系， 而其他没有因果关系的数据，可以允许不一致。
可串行化一致性（ Serializable Consistency)
如果说操作的历史等同于以某种单一原子顺序发生的历史，但对调用和完 成时间没有说明，那么就可以获得称为可序列化的一致性模型。这个模型很有 意思，一致性要么比你想象的强得多，要么弱得多。 可串行化一致性很弱，由于它没有按时间或顺序排列界限，因此这就好像 消息可以任意发送到过去或未来。例如，在一个可序列化的系统中，有如下所 示的这样一个程序：
1
2
3
x ~ 1
x = x + 1
puts x
在这里，我们假设每行代表一个操作，并且所有的操作都成功。因为这些操作可以以任何顺序进行，所以可能打印出 nil、1 或 2 。因此，一致性显得很弱。
但在另一方面，串行化的一致性又很强，因为它需要一个线性顺序。例如，下面的这个程序：
1
2
3
4
print x if x = 3
x = 1 if x = nil
x = 2 if x = 1
x=3 if x=2
它可能不会严格地以我们编写的顺序发生，但它能够可靠地将 x 从 nil → 1 → 2 ，更改为 3 ，最后打印出 3。因此，可序列化允许对操作重新进行任意排序，只要顺序看起来是原子的即可。
以用户为中心的一致性模型
在实际业务需求中，很多时候并不会要求系统内所有的数据都保持一致，例如在线的日记本，业务只要求基于这个用户满足一致性即可，而不需要关心整体。这就是所谓的以用户为中心的一致性。
最终一致性（Eventual Consistency)
在读多写少的场景中，例如CDN ，读写之比非常悬殊，如果网站的运营人员修改了一张图片，最终用户延迟了一段时间才看到这个更新实际上问题并不是很大。我们把这种一致性归结为最终一致性。最终一致性是指如果更新的间隔时间比较长，那么所有的副本都能够最终达到一致性。
最终一致性是弱一致性的一种特例，在弱一致性情况下，用户读到某一操作对系统特定数据的更新需要一段时间，我们将这段时间称为“ 不一致性窗口”。
在最终一致性的情况下，系统能够保证用户最终将读取到某操作对系统特定数据的更新（读取操作之前没有该数据的其他更新操作） 。此种情况下，如果没有发生失败，那么“不一致性窗口”的大小将依赖于交互延迟、系统的负载，以及复制技术中副本的个数（可以理解为master/slave 模式中s lave 的个数） 。DNS 系统在最终一致性方面可以说是最出名的系统，当更新一个域名的IP 以后，根据配置策略以及缓存控制策略的不同，最终所有的客户都会看到最新的值。
最终一致性模型根据其提供的不同保证可以划分为更多的模型， 比如上文提到的因果一致性（Causal Consistency）就是其中的一个分支。
