跳表是一种有序数据结构，它通过在每个节点中维持多个指向其他节点的指针作为索引，实现高效范围查询。
简单说明
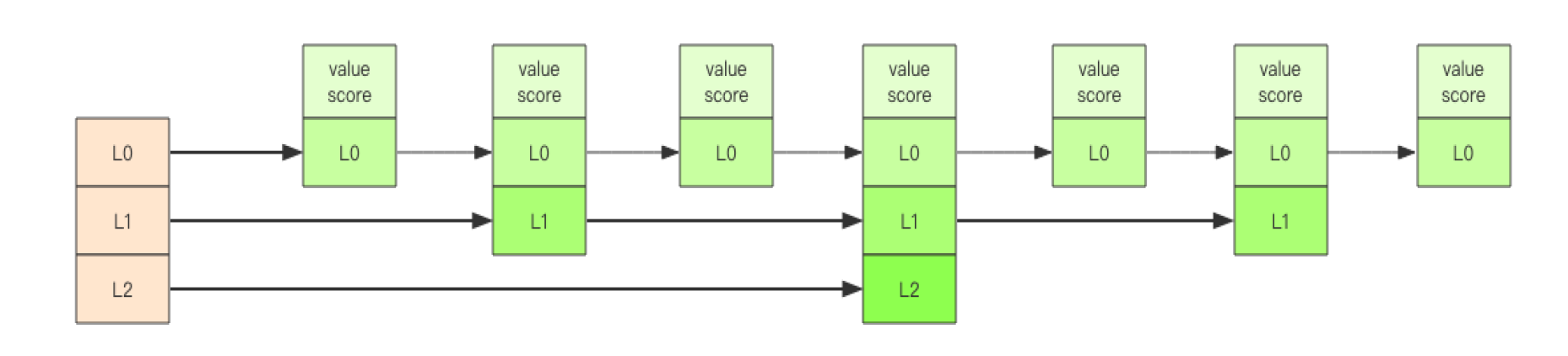跳跃列表类似于层级制，最下面一层所有的元素都会串起来。然后每隔几个元素挑选出一个代表来，再将这几个代表使用一级指针串起来。然后在这些代表里再挑出二级代表，再串起来。以此类推，最终就形成了金字塔结构。
跳跃列表之所以「跳跃」，是因为内部的元素可能「身兼数职」，比如上图中间的这个元素，同时处于 L0、L1 和 L2 层，可以快速在不同层次之间进行「跳跃」。
插入过程
定位插入点时，先在顶层进行定位，然后下潜到下一级定位，一直下潜到最底层找到合适的位置，将新元素插进去。
跳跃列表采取一个随机策略来决定新元素可以兼职到第几层。首先L0层肯定是100%了，L1层只有50%的概率，L2层只有25%的概率，L3层只有12.5%的概率，一直随机到最顶层L31层。绝大多数元素都过不了几层，只有极少数元素可以深入到顶层。列表中的元素越多，能够深入的层次就越深，能进入到顶层的概率就会越大。
查找过程
设想如果跳跃列表只有一层会怎样？插入删除操作需要定位到相应的位置节点 (定位到最后一个比「我」小的元素，也就是第一个比「我」大的元素的前一个)，定位的效率肯定比较差，复杂度将会是O(n)，因为需要挨个遍历。也许你会想到二分查找，但是二分查找的结构只能是有序数组。跳跃列表有了多层结构之后，这个定位的算法复杂度将会降到 O(lg(n))。
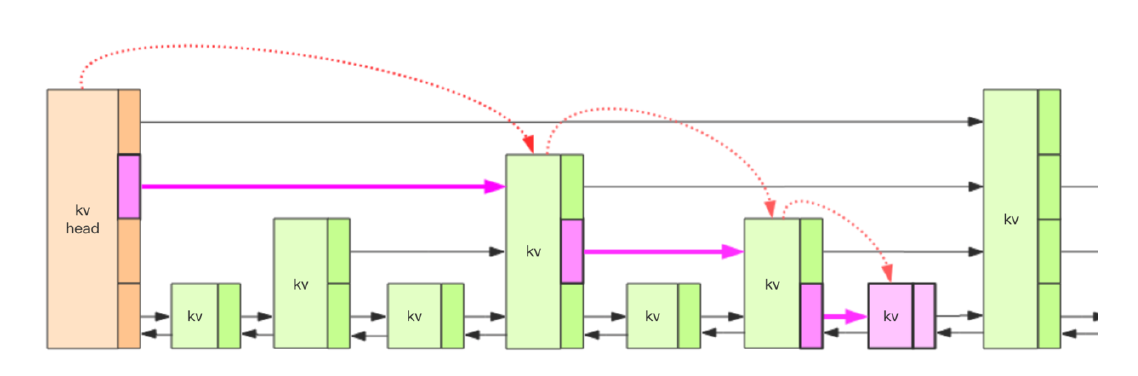
如图所示，我们要定位到那个紫色的kv，需要从 header 的最高层开始遍历找到第一个节点 (最后一个比「我」小的元素)，然后从这个节点开始降一层再遍历找到第二个节点 (最后一个比「我」小的元素)，然后一直降到最底层进行遍历就找到了期望的节点 (最底层的最后一个比我「小」的元素)。 我们将中间经过的一系列节点称之为「搜索路径」，它是从最高层一直到最底层的每一层最后一个比「我」小的元素节点列表。 有了这个搜索路径，我们就可以插入这个新节点了。不过这个插入过程也不是特别简单。因为新插入的节点到底有多少层，得有个算法来分配一下，跳跃列表使用的是随机算法。
随机层数
对于每一个新插入的节点，都需要调用一个随机算法给它分配一个合理的层数。直观上期望的目标是50%的Level1，25% 的Level2，12.5%的Level3，一直到最顶层2^-63，因为这里每一层的晋升概率是50%。
不过Redis标准源码中的晋升概率只有25%，也就是代码中的ZSKIPLIST_P的值。所以官方的跳跃列表更加的扁平化，层高相对较低，在单个层上需要遍历的节点数量会稍多一点。
也正是因为层数一般不高，所以遍历的时候从顶层开始往下遍历会非常浪费。跳跃列表会记录一下当前的最高层数maxLevel，遍历时从这个maxLevel开始遍历性能就会提高很多。
代码实现
typedef struct zskiplist {
struct zskiplistNode *header, *tail;//header指向跳跃表的表头节点，tail指向跳跃表的表尾节点
unsigned long length; //跳跃表的长度或跳跃表节点数量计数器，除去第一个节点
int level; //跳跃表中节点的最大层数，除了第一个节点
} zskiplist;
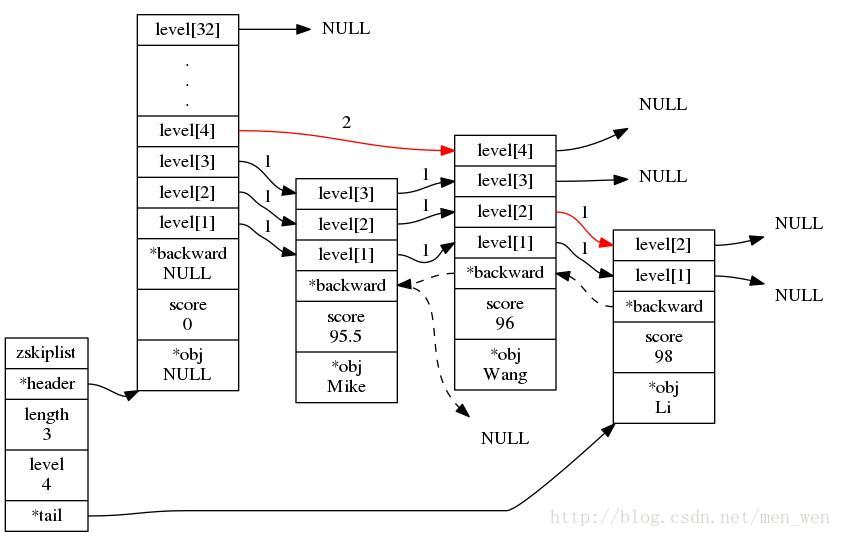上图就是跳跃列表的示意图，Redis的跳跃表共有 64 层，意味着最多可以容纳 2^64 个元素。每一个 kv 块对应的结构如下面的代码中的 zslnode 结构，kv header也是这个结构，只不过 value 字段是无效的 null 值，score 是 Double.MIN_VALUE 用来垫底的。kv 之间使用指针串起来形成了双向链表结构，它们是有序排列的，从小到大。不同的 kv 层高可能不一样，层数越高的 kv 越少。同一层的kv会使用指针串起来。每一个层元素的遍历都是从 kv header 出发。
1
2
3
4
5
6
7
8
9
typedef struct zskiplistNode {
robj *obj; //保存成员对象的地址
double score; //分值
struct zskiplistNode *backward; //后退指针
struct zskiplistLevel {
struct zskiplistNode *forward; //前进指针
unsigned int span; //跨度
} level[]; //层级，柔型数组
} zskiplistNode;
