概念
二叉堆是一种特殊的堆。具有如下的特性:
- 具有完全二叉树的特性。
- 堆中的任何一个父节点的值都大于等于它左右孩子节点的值,或者都小于等于它左右孩子节点的值。
其主要操作就两个, sink (下沉)和 swim (上浮),⽤以维护⼆叉堆的性质。其主要应⽤有两个,⾸先是⼀种排序⽅法「堆排序」,第⼆是⼀种很有⽤的数据结构「优先级队列」。
根据第二条特性,我们又可以把二叉堆分成两类:
- 最大堆: 父节点的值大于等于左右孩子节点的值
- 最小堆: 父节点的值小于等于左右孩子节点的值
⼆叉堆其实就是⼀种特殊的⼆叉树(完全⼆叉树),只不过存储在数组⾥。⼀般的链表⼆叉树,我们操作节点的指针,⽽在数组⾥,我们把数组索引作为指针
实现
存储结构是数组,将数组维护成逻辑上的完全二叉树。在二叉堆中插入和删除、查找的时间复杂度都是log(n)
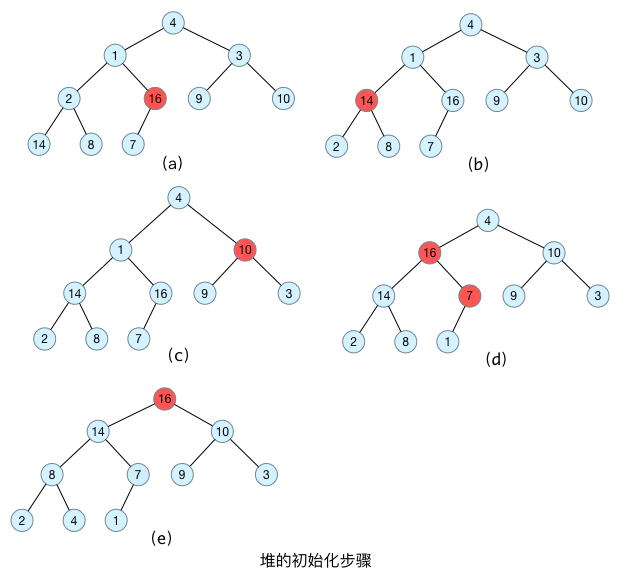
构建堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public static void buildMaxHeap(int[] array) {
if (array == null || array.length == 1)
return;
// 堆的公式 是 int root = i, int left = 2*i+1, int right = 2*i+2;
// 获取第一个非叶子节点
int cursor = (array.length / 2) - 1;
for (int i = cursor; i >= 0; i--) { // 这样for循环下,就可以第一次排序完成
// maxHeap(array, array.length, i);
minHeap(array, array.length, i);
}
}
// 最小堆
public static void minHeap(int[] array, int heapSieze, int index) {
int left = index * 2 + 1; // 左子节点
int right = index * 2 + 2; // 右子节点
int maxValue = index; // 暂时定在Index的位置就是最小值
// 如果左子节点的值,比当前最小的值小,就把最小值的位置换成左子节点的位置
if (left < heapSieze && array[left] < array[maxValue]) {
maxValue = left;
}
// 如果右子节点的值,比当前最小的值小,就把最小值的位置换成左子节点的位置
if (right < heapSieze && array[right] < array[maxValue]) {
maxValue = right;
}
// 如果不相等,说明这个子节点的值有比自己小的,位置发生了交换了位置
if (maxValue != index) {
swap(array, index, maxValue); // 就要-交换位置元素
// 交换完位置后还需要判断子节点是否打破了最小堆的性质。最小性质:两个子节点都比父节点大。
minHeap(array, heapSieze, maxValue);
}
}
// 数组元素交换
public static void swap(int[] array, int index1, int index2) {
int temp = array[index1];
array[index1] = array[index2];
array[index2] = temp;
}
堆排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static void heapSort(int[] array) {
if (array == null || array.length == 1)
return;
buildMaxHeap(array); // 第一次排序,构建最大堆,只保证了堆顶元素是数组里最大的
for (int i = array.length - 1; i >= 1; i --) {
// 经过上面的一些列操作,目前array[0]是当前数组里最大的元素,需要和末尾的元素交换
// 然后,拿出最大的元素
swap(array, 0, i);
// 交换完后,下次遍历的时候,就应该跳过最后一个元素,也就是最大的那个值,然后开始重新构建最大堆
// 堆的大小就减去1,然后从0的位置开始最大堆
// maxHeap(array, i, 0);
minHeap(array, i, 0);
}
}
插入
插入位置是完全二叉树的最后一个位置。在插入结点后需要对堆进行调整。调整方法为(对于小顶堆而言):将插入的结点与其父结点比较,若小于其父结点的值,则交换两者。重复此操作,直至该结点不比其父结点小,或者该结点成为根结点。可以通过插入结点到一个已经存在的堆中,也可以通过不断插入结点来构建一个堆。
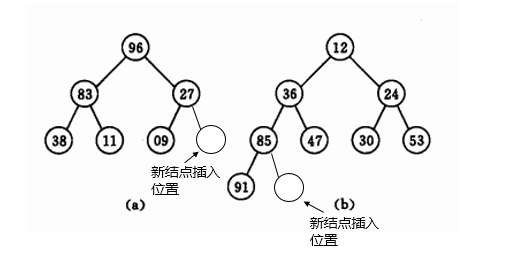
删除
删除节点一般删除的是根节点。把根节点删除之后,用二叉堆的最后一个元素顶替上来,然后在进行调整恢复。
应用场景
优先级队列
优先级队列这种数据结构有⼀个很有⽤的功能,当插⼊或者删除元素的时候,元素会⾃动排序,这底层的原理就是⼆叉堆的操作。
数据结构的功能⽆⾮增删改查,优先级队列有两个主要 API,分别是 insert 插⼊⼀个元素和 delMax 删除最⼤元素(如果底层⽤最⼩堆,那么就是 delMin )。